벨만 포드(Bellman Ford) 알고리즘

[ 벨만 포드(Bellman Ford) ]

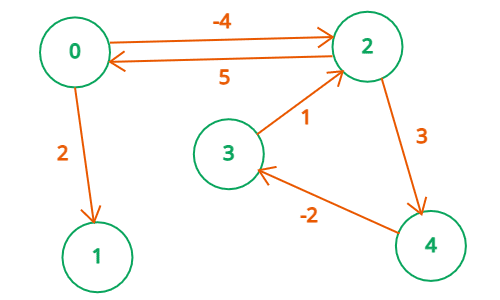
벨만 포드(Bellman Ford) 알고리즘은 그래프의 한 노드에서 다른 모든 노드까지의 최단 경로를 구할 수 있는 알고리즘이다. 최단 경로 알고리즘 중 하나인 다익스트라 알고리즘(https://goo-gy.github.io/2019-10-11-dijkstra)보다 높은 시간 복잡도를 가진다. 대신 다익스트라 알고리즘은 그래프에 음수 cost가 있는 경우에는 사용할 수 없는 반면, Bellman Ford 알고리즘은 음수 cost가 있는 경우에도 사용할 수 있다.

• 음수 cost 그래프에서 적용 가능
• Negative Cycle 감지 가능
• 시간 복잡도 = O(NE)
  N(Node의 수), E(Edge의 수)

알고리즘

1. 출발 노드 설정 & 최단 거리 테이블 초기화
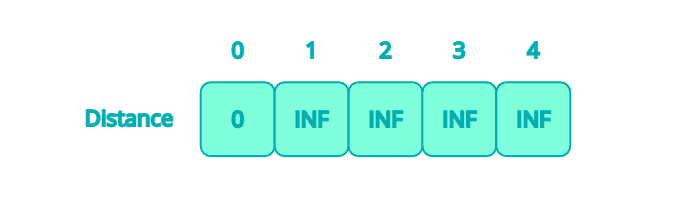   최단 거리 테이블의 기본값은 무한(INF), 출발 노드는 0으로 초기화
2. 모든 Edge를 순회하면서 distance[src] + cost < distance[dst] 라면 업데이트
3. 2번을 N - 1 번 반복

증명

다른 부분을 제외하고 출발지에서 임의의 노드로의 최단 경로만 살펴보자.

최단 경로 순서대로 Edge를 순회한다면, 위 2번 과정을 한 번만 수행해도 최단 거리가 갱신된다.

최악의 경우에도 2번 과정을 한 번 수행하면 최단 경로에 포함된 두 번째 노드의 최단 거리는 갱신된다.

마찬가지로 2번 과정을 한 번 수행할 때마다, 최단 경로에 있는 노드가 차례로 하나씩 최단 거리를 보장하게 된다. 그래프의 노드 수가 N이라면 2번 과정을 N - 1번만 수행하면 그래프 내 모든 노드까지의 최단 경로를 갱신할 수 있다.

Negative Cycle

위 증명은 그래프 내에 cost의 합이 음수가 되는 Negative Cycle이 없다고 가정했을 경우에 성립한다.

그림처럼 경로 상에 Negatvie Cycle이 있다면, 최단 경로를 구하기 위해 Negative Cycle을 무한히 순회해야 하기 때문에 최단 경로를 정의하기 어렵다. 굳이 최단 거리를 따지자면 -∞이 될 것이다.

• 그래프에 Negative Cycle이 존재하는지는 어떻게 알 수 있을까.
  위에서 Negative Cycle이 없을 경우 Edge를 N - 1번 순회하며 출발지에서 모든 노드까지의 최단 거리를 갱신할 수 있었다. 최단 거리가 갱신된 노드는 Distance가 업데이트될 일이 없다. 따라서 그 이후 2번 과정을 더 수행하였을 때, 어떤 노드든 Distance가 업데이트된다면 그래프 내에 Netgative Cycle이 있음을 알 수 있다.

[ 코드 ]

bool bellman_ford()
{
    distance_map[1] = 0;
    for(int n = 1; n <= N; n++)
    {
        for(map<pair<int,int>, long long>::iterator e = loads.begin(); e != loads.end(); e++)
        {
            int src = e->first.first;
            int dst = e->first.second;
            long long weight = e->second;
            if(distance_map[src] != INF && distance_map[dst] > distance_map[src] + weight)
            {
                distance_map[dst] = distance_map[src] + weight;
                if(n == N)
                    return true;
            }
        }
    }
    return false;
}

N번째에서 순회에서 Distance가 업데이트 될 경우 true(Negative Cycle 있음)를 리턴한다.