algorithm11 October, 2019

다익스트라 (Dijkstra)

[ 최단거리 찾기 ]

거리 비용이 같은 맵에서 최단거리 찾기

ex) 타일 게임에서 최단 경로 찾기
노드마다 다른 거리 비용을 가지는 맵에서 최단거리 찾기

ex) STAGE마다 클리어에 필요한 시간 비용이 다른 STAGE 맵에서 최단 시간
간선마다 다른 거리 비용을 가지는 그래프에서 최단거리 찾기
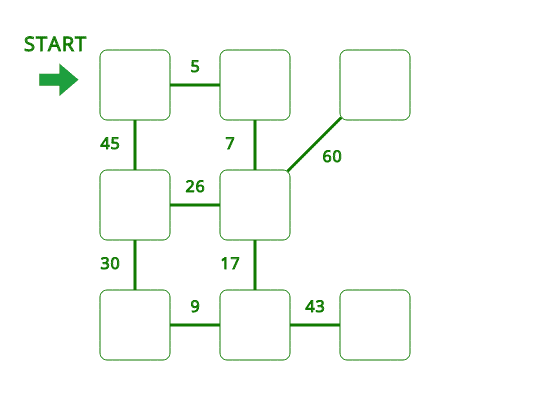
Dijkstra 알고리즘으로 해결할 수 없는 경우
음수의 거리 비용이 존재할 경우에는 다익스트라(Dijkstra) 알고리즘을 사용할 수 없습니다. 자세한 이유는 뒤에 [ 증명 ]에서 설명하겠습니다.

[ 다익스트라(Dijkstra) 알고리즘 ]

다익스트라(Dijkstra) 알고리즘은 지정한 한 노드에서 접근 가능한 모든 노드까지의 최단 거리를 구할 수 있는 알고리즘입니다. 방법은 다음과 같습니다.

초기화
먼저 각 노드들의 출발점으로부터의 거리를 기록할 테이블을 만듭니다. (모든 값을 INF(무한대라고 볼 수 있는 굉장히 큰 수)로 초기화합니다.)
출발지의 기록 거리를 업데이트하고 출발지를 현재 노드로 선택합니다.
현재 노드와 인접한 노드들의 기록 거리를 업데이트합니다.

※초록색 노드는 방문된 노드입니다.
※노란색 노드는 대기열에 있는 노드입니다.
현재 노드는 CHECK 표시를 하여 다시 방문하는 일이 없도록 합니다.
[현재 노드의 기록 거리 + 인접 노드까지의 거리] < [인접 노드의 기록 거리] 경우에만 업데이트합니다.
업데이트에 성공한 노드들을 대기열에 넣습니다.
대기열에서 기록 거리가 가장 작은 노드를 꺼내 현재 위치로 정합니다. (우선순위 큐를 이용할 수 있습니다.)
[37, 98]에서 37로 가장 작은 거리를 가지는 [1][0] 노드를 꺼내서 방문합니다.

[40, 50, 98]에서 40으로 가장 작은 거리를 가지는 [2][0] 노드를 꺼내서 방문합니다.
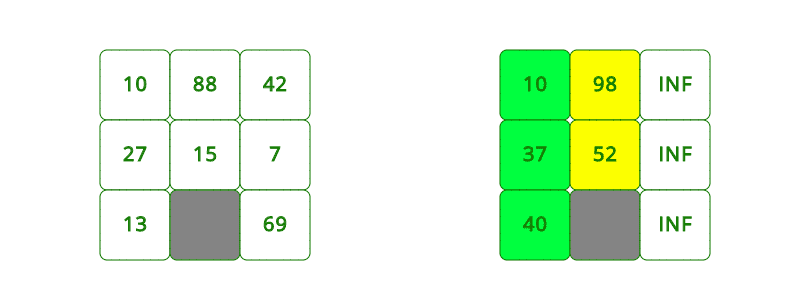
1,2를 대기열이 빌 때까지 반복합니다.

[ 증명 ]

경로가 있는 모든 노드를 방문하는가?
인접한 노드의 업데이트가 성공하면 해당 노드를 대기열에 넣습니다. 각 노드의 기록 거리 초깃값은 INF이기 때문에 길이 막혀있지 않는 한 모든 노드를 한 번씩은 방문합니다.
방문된 노드의 기록 거리가 최단거리인가?
임의의 노드 A를 방문할 때 대기열에서 기록 거리가 가장 짧은 노드를 꺼낸 것이 A입니다. 즉 큐에 있는 다른 노드를 거쳐서 A에 도착할 경우 분명히 더 크거나 같은 거리 비용이 소요됩니다.
※ 거리 비용이 음수인 값이 있을 경우에는 성립하지 않기 때문에 Dijkstra 알고리즘을 사용할 수 없습니다.
A 방문 이후에 업데이트되는 기록 거리는 A의 기록 거리보다 크기 때문에 A의 기록 거리가 수정될 일은 없습니다.

[ 코드 ]

from queue import PriorityQueue

INF = 9999 # 입력 범위를 고려하여 충분히 큰 값으로 설정합니다.  
X = 0
Y = 1

def tuple_sum(tuple_a, tuple_b):
  tuple_sum = tuple(sum(elem) for elem in zip(tuple_a, tuple_b))
  return tuple_sum
  
def set_distance(distance_map, load_map, checked_map, current_point, next_point):
  m = len(load_map)
  n = len(load_map[0])
  if(next_point[Y] < 0 or next_point[X] < 0 or next_point[Y] >= m or next_point[X] >= n):
      return False
  if(load_map[next_point[Y]][next_point[X]] == 0):
      return False
  if(checked_map[next_point[Y]][next_point[X]]):
      return False
  update_distance = distance_map[current_point[Y]][current_point[X]] + load_map[next_point[Y]][next_point[X]]
  if(distance_map[next_point[Y]][next_point[X]] > update_distance):
      distance_map[next_point[Y]][next_point[X]] = update_distance
      return True
  else:
      return False
  
def solution(load_map):
  m = len(load_map)
  n = len(load_map[0])
  
  distance_map = [[INF for j in range(n)] for i in range(m)]
  distance_map[0][0] = 0
  checked_map = [[False for j in range(n)] for i in range(m)]
  MOVES = [(1,0), (0,1), (-1,0), (0,-1)]
  start_point = (0, 0)
  
  next_queue = PriorityQueue()
  next_queue.put([distance_map[0][0], start_point])
  while(not next_queue.empty()):
      current_point = next_queue.get(0)[1]

      checked_map[current_point[Y]][current_point[X]] = True
      for move in MOVES:
          next_point = tuple_sum(current_point, move)
          if(set_distance(distance_map, load_map, checked_map, current_point, next_point)):
              next_queue.put([distance_map[next_point[Y]][next_point[X]], next_point])
  return distance_map

if(__name__ == "__main__"):
  load_map = [[ 1,50, 2, 1,31],
              [93, 0, 0, 0,12],
              [ 1,30,19, 7,87],
              [20, 5,39,15,86],
              [ 0, 0, 0,27,45]]
  result = solution(load_map)
  for row in result:
      for node in row:
          print("%4d" %node, end=" ")
      print("")

[ 유형별 차이 살펴보기 ]

거리 비용이 같은 맵에서 최단거리 찾기
거리 비용이 모두 같은 맵에서는 굳이 우선순위 큐를 사용할 필요가 없습니다. 이동한 깊이가 곧 거리가 되기 때문에 너비 우선 탐색(BFS)으로만 탐색해도 먼저 도착한 경로가 최단 경로가 됩니다.
노드마다 다른 거리 비용을 가지는 맵에서 최단거리 찾기
이 경우에는 우선순위 큐가 필요하지만 한번 업데이트된 노드의 기록 거리를 덮어쓸 일은 없습니다. 왜냐면 어느 방향에서 들어오던 특정 노드에 진입하는데 필요한 거리 비용은 같기 때문에 먼저 접근하는 노드가 더 작은 기록 거리를 가지고 있습니다. 따라서 최초의 업데이트가 최단 거리를 기록하게 됩니다.
간선마다 다른 거리 비용을 가지는 그래프에서 최단거리 찾기
하지만 간선마다 거리 비용이 다르다면 이야기가 다릅니다.

그림처럼 B의 기록 거리가 C의 기록 거리보다 작더라도 [C의 기록 거리 + C-A의 거리 비용] < [B의 기록 거리 + B-A 거리 비용]일 경우 C를 방문할 때 이미 업데이트되어 있는 A의 기록 거리를 덮어쓰게 됩니다.

[ 최단거리 찾기 ]

[ 다익스트라(Dijkstra) 알고리즘 ]

[ 증명 ]

[ 코드 ]

[ 유형별 차이 살펴보기 ]

googy