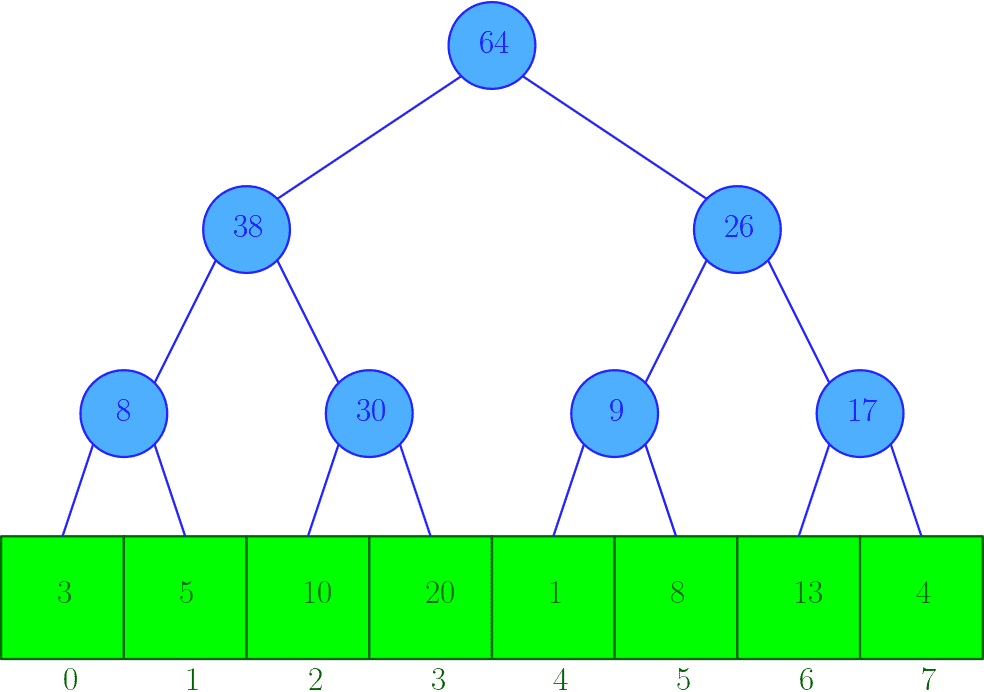
인덱스 트리(Index Tree)
구간 합 알고리즘
인덱스 트리가 해결할 수 있는 가장 대표적인 문제는 구간 합 문제이다. 구간 합을 구하는 전형적인 알고리즘은 다음과 같다.
- 구간을 순회하여 더하기
- 처음부터 index까지의 합을 저장하는 서브 배열 만들기
- 인덱스 트리
- 세그먼트 트리
구간을 순회하여 더하기
이 방법은 가장 단순한 방법으로 시간복잡도는 O(N)이다. 하지만 구간 합을 K번 구해야 한다면 시간복잡도는 O(K*N)이 된다.
합을 저장하는 서브 배열 만들기
이 방법은 구간 합을 여러 번 구해야 할 때 효율적이다.
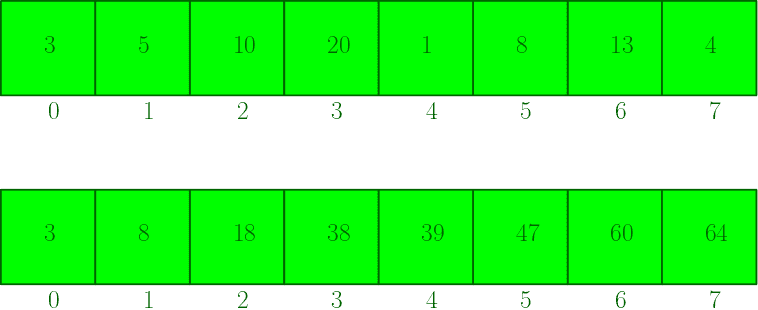
서브 배열을 만들어 처음부터 K의 합을 sub[K]에 저장한다. 그러면 뺼셈 한 번으로 구간 합을 구할 수 있다. 따라서 O(1)로 수행할 수 있고, 구간 합을 K번 구할 때의 시간복잡도는 O(N + K)가 된다.
하지만, 배열에 저장된 값이 수시로 업데이트된다면, 업데이트가 일어날 때마다 구간 합을 다시 저장해야 하며 그때마다 O(N)의 작업이 필요하다.
인덱스 트리(Index Tree)
인덱스 트리는 처음 트리를 구성할 때 O(N)의 작업이 필요하다. 그러면 이후에 데이터를 조회할 때도 O(log N) 만에 수행할 수 있고, 배열의 데이터가 수정되어도 O(log N)만에 트리를 업데이트할 수 있다. 따라서 앞에서처럼 데이터가 자주 업데이트되는 경우에 유용하게 사용할 수 있다. 인덱스 트리는 구간 합이 아닌 구간 Max, Min 등 다양한 목적으로도 사용할 수 있다.
구현
구간 합을 위한 인덱스 트리는 인접한 두 노드의 합을 부모 노드에 저장하여 트리를 구성한다. 인덱스 트리는 일반적으로 완전 이진 트리를 이용해 구현한다.
구간 합 구하기
- left, right를 구간의 시작 노드, 끝 노드로 설정한다.
- left는 오른쪽 위 노드를, right는 왼쪽 위 노드를 next로 설정한다.
- 각각의 next가 부모 노드가 아니라면 현재 노드 value를 sum에 더한다.
- left, right를 각각의 next로 이동한다.
- left >= right일 때까지 2,3,4를 반복한다.
- left == right라면 해당 노드도 sum에 더한다.
데이터 업데이트
배열의 데이터가 수정이 일어나면 모든 트리를 수정할 필요 없이 자신과 연결된 조상 노드들만 업데이트해 주면 된다. 따라서 업데이트도 O(log N) 만에 수행할 수 있다.
Code
Index tree를 문제를 풀기 위해 만들어 둔 code snippet을 가져왔다. Index tree를 쓰는 것만으로도 code 규모가 꽤나 크고, 정형화된 변수와 로직이 있기 때문에 class로 제작하였다.
#include <vector>
using namespace std;
class IndexTree
{
public:
int leafLeft;
int treeSize;
vector<long long> v_tree;
IndexTree(int N)
{
for (leafLeft = 1; leafLeft < N; leafLeft *= 2)
;
treeSize = leafLeft * 2;
v_tree.resize(treeSize);
}
long long logicFun(long long num1, long long num2)
{
// TODO : set logic
return num1 + num2;
}
void updateTree(int index)
{
if (index == 0)
return;
v_tree[index] = logicFun(v_tree[2 * index], v_tree[2 * index + 1]);
updateTree(index / 2);
}
void update(int order, long long data)
{
int index = leafLeft + order - 1;
v_tree[index] = data;
updateTree(index / 2);
}
long long query(int begin, int end)
{
int L = leafLeft + begin - 1;
int R = leafLeft + end - 1;
// TODO: set initial
long long result = 0;
while (L < R)
{
int nextL = (L + 1) / 2;
int nextR = (R - 1) / 2;
if (nextL != L / 2)
result = logicFun(result, v_tree[L]);
if (nextR != R / 2)
result = logicFun(result, v_tree[R]);
L = nextL;
R = nextR;
}
if (L == R)
result = logicFun(result, v_tree[L]);
return result;
}
};