위상 정렬 (Topological Sort)
위상 정렬 (Topological Sort)
위상 정렬은 사이클이 없는 방향 그래프 (Directed Acyclic Graphs)에서 순서를 거스르지 않고 모든 노드를 나열하는 알고리즘으로 선후 관계(전제 조건)를 지키면서 일의 순서를 결정하는 데 사용할 수 있다. 결과적으로 보았을 때 그냥 정렬 알고리즘처럼 보이지만, 값의 비교가 아닌 두 작업의 관계에서 순서가 정해지는 경우에 위상 정렬 알고리즘을 사용하여 해결할 수 있다.
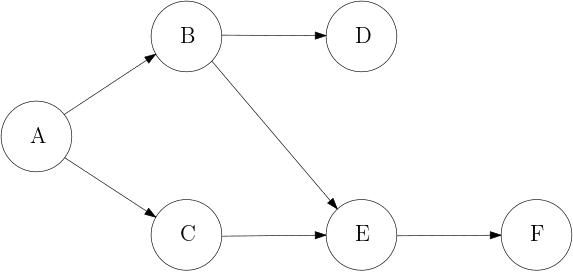
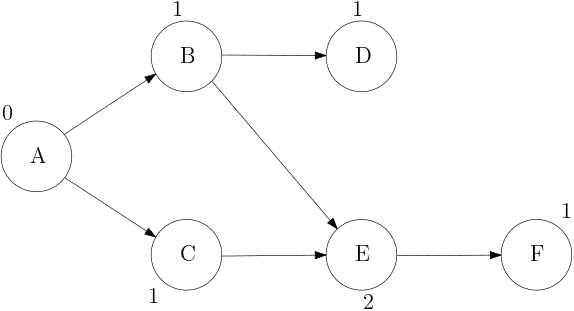
위 그래프의 경우 A와 B의 순서는 비교할 수 있지만, A와 E만을 보았을 때는 두 노드의 순서를 결정할 수 없다. 따라서 일반적인 정렬 알고리즘을 적용할 수 없고 위상 정렬 알고리즘을 사용해야 한다.
알고리즘
위상 정렬 알고리즘의 핵심은 전제 조건이 없는 (진입 차수가 0인) 작업을 먼저 수행하고, 그 일을 수행함으로써 전제 조건이 만족되는 작업들을 순서대로 수행하는 것이다.
'진입 차수'란 해당 노드를 가리키는 Edge의 개수를 뜻한다. 위 그래프의 경우 A의 진입 차수는 0, E의 진입 차수는 2이다.
위상 정렬 단계
위상 정렬 알고리즘을 간단하게 정리한다면 다음과 같다.
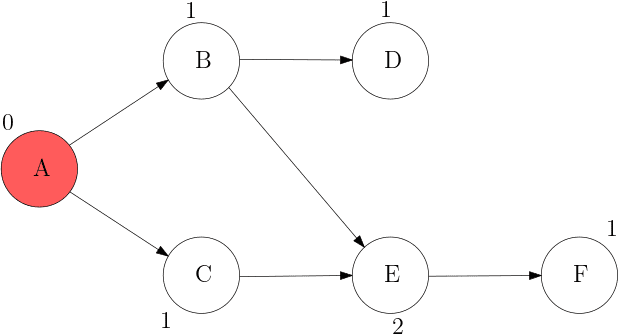
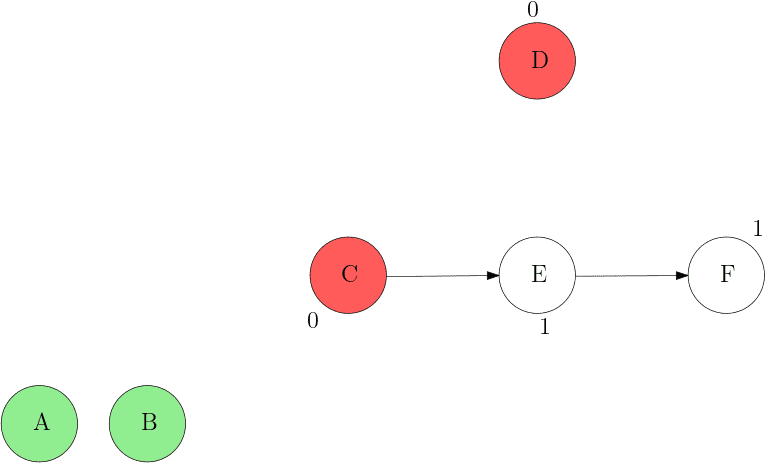
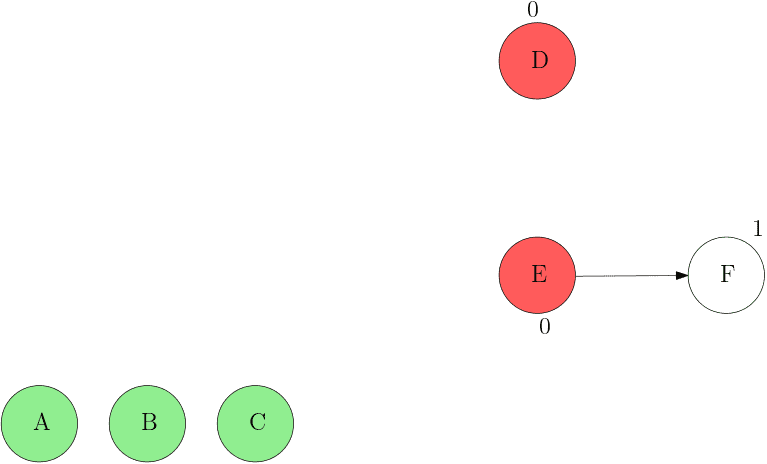
1. 진입 차수가 0인 노드를 모두 Queue에 삽입한다.
2. Queue에서 노드를 꺼내 방문한다.
- 연결된 Edge을 모두 제거한다.
- 이때 진입 차수가 0이 된 노드를 Queue에 삽입한다.
3. 모든 노드를 방문할 때까지 2를 반복한다.
눈치채신 분들도 있겠지만, 진입 차수가 0이 되는 노드가 동시에 여러 개 발생한다면 Queue에 무엇을 먼저 넣느냐에 따라서 결과가 달라질 수 있다. 하지만 별다른 조건이 없다면 이들은 모두 정답이 될 수 있다.
예제
위상 정렬 알고리즘을 적용하여 [BAEK-JOON 1766] 문제를 풀어보자.
먼저 푸는 것이 좋은 문제가 있는 문제는, 먼저 푸는 것이 좋은 문제를 반드시 먼저 풀어야 한다. 라는 조건은 위상 정렬을 이용하면 된다.
하지만 다른 조건 가능하면 쉬운 문제부터 풀어야 한다. 도 만족시키기 위해 Queue 대신 Priority Queue를 사용하였다.
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
int N, M;
vector<vector<int>> vv_graph;
vector<int> v_degree;
void solution()
{
priority_queue<int, vector<int>, greater<int>> pq_node;
for (int i = 1; i <= N; i++)
{
if(v_degree[i] == 0)
pq_node.push(i);
}
while(!pq_node.empty())
{
int cur = pq_node.top(); pq_node.pop();
cout << cur << " ";
for(int dst : vv_graph[cur])
{
v_degree[dst]--;
if(v_degree[dst] == 0)
pq_node.push(dst);
}
}
cout << "\n";
}
void input()
{
cin >> N >> M;
vv_graph.resize(N + 1);
v_degree.resize(N + 1);
for (int i = 1; i <= M; i++)
{
int src, dst;
cin >> src >> dst;
vv_graph[src].push_back(dst);
v_degree[dst]++;
}
}
void pre_setting()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
}
int main()
{
pre_setting();
input();
solution();
return 0;
}