
[ Floyd Warshall ]
Floyd Warshall 알고리즘은 모든 노드에서 모든 노드까지의 최단 경로를 구할 수 있는 알고리즘이다.
- 시간 복잡도 = O(N^3)
- 가중치가 음수인 Edge가 존재할 때도 적용 가능
- 음수 Cycle 감지
N(Node의 수)
[ 알고리즘 ]
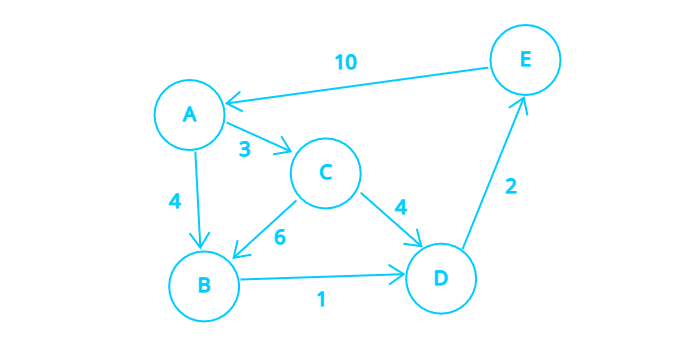
과정
단계별 과정
|
A |
B |
C |
D |
E |
| A |
0 |
4 |
3 |
INF |
INF |
| B |
INF |
0 |
INF |
1 |
INF |
| C |
INF |
6 |
0 |
4 |
INF |
| D |
INF |
INF |
INF |
0 |
2 |
| E |
10 |
INF |
INF |
INF |
0 |
A를 거쳐가는 경우 업데이트
|
A |
B |
C |
D |
E |
| A |
0 |
4 |
3 |
INF |
INF |
| B |
INF |
0 |
INF |
1 |
INF |
| C |
INF |
6 |
0 |
4 |
INF |
| D |
INF |
INF |
INF |
0 |
2 |
| E |
10 |
14 |
13 |
INF |
0 |
B를 거쳐가는 경우 업데이트
|
A |
B |
C |
D |
E |
| A |
0 |
4 |
3 |
5 |
INF |
| B |
INF |
0 |
INF |
1 |
INF |
| C |
INF |
6 |
0 |
4 |
INF |
| D |
INF |
INF |
INF |
0 |
2 |
| E |
10 |
14 |
13 |
15 |
0 |
C를 거쳐가는 경우 업데이트
|
A |
B |
C |
D |
E |
| A |
0 |
4 |
3 |
5 |
INF |
| B |
INF |
0 |
INF |
1 |
INF |
| C |
INF |
6 |
0 |
4 |
INF |
| D |
INF |
INF |
INF |
0 |
2 |
| E |
10 |
14 |
13 |
15 |
0 |
D를 거쳐가는 경우 업데이트
|
A |
B |
C |
D |
E |
| A |
0 |
4 |
3 |
5 |
7 |
| B |
INF |
0 |
INF |
1 |
3 |
| C |
INF |
6 |
0 |
4 |
6 |
| D |
INF |
INF |
INF |
0 |
2 |
| E |
10 |
14 |
13 |
15 |
0 |
E를 거쳐가는 경우 업데이트
|
A |
B |
C |
D |
E |
| A |
0 |
4 |
3 |
5 |
7 |
| B |
13 |
0 |
16 |
1 |
3 |
| C |
16 |
6 |
0 |
4 |
6 |
| D |
12 |
16 |
15 |
0 |
2 |
| E |
10 |
14 |
13 |
15 |
0 |
[ 코드 ]
for middle in range(1, N + 1):
for src in range(1, N + 1):
for dst in range(1, N + 1):
if(src == dst):
continue
new_cost = load_map[src][middle] + load_map[middle][dst]
if(new_cost < load_map[src][dst]):
load_map[src][dst] = new_cost
