트리 (Tree)

[ 개념 및 구조 ]

트리는 계층적인 형태를 가지고 있는 자료구조입니다.

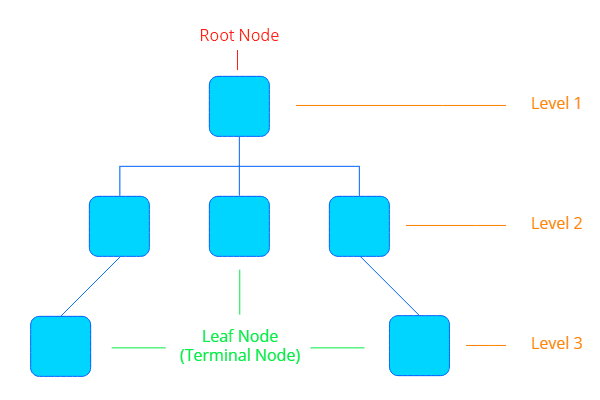
트리에서 가장 꼭대기에 위치해 부모 노드가 없는 노드를 루트 노드(Root Node)라고 합니다.
트리에서 가장 끝에 위치해 자식이 없는 노드를 리프 노드(Leaf Node) 혹은 단말 노드(Terminal Node)라고 합니다.
트리는 레벨(Level)이라는 개념이 있는데 이는 루트 노드에서 1로 시작하고 자식 노드를 따라 아래로 내려갈 때마다 1씩 증가합니다.

• 노드(Node)
• 자식 노드(Child Node)
• 부모 노드(Parent Node)
• 형제 노드(Sibling Node)
• 루트 노드(Root Node)
• 리프 노드(Leaf Node)[= 단말 노드(Terminal Node)]
• 내부 노드(Internal Node)
• 레벨(Level)

[ 이진 트리 (Binary Tree) ]

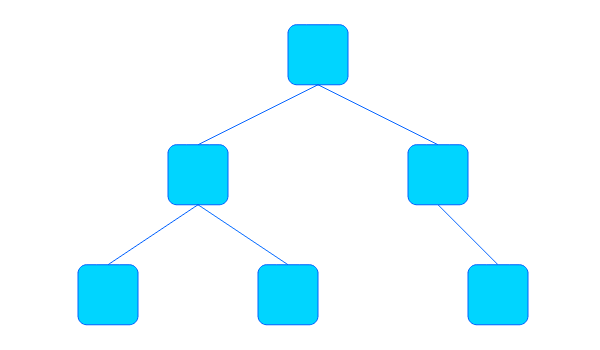
각 노드마다 최대 2개의 자식을 가질 수 있는 트리를 이진 트리라고 합니다.

• 포화 이진 트리(Full Binary Tree)
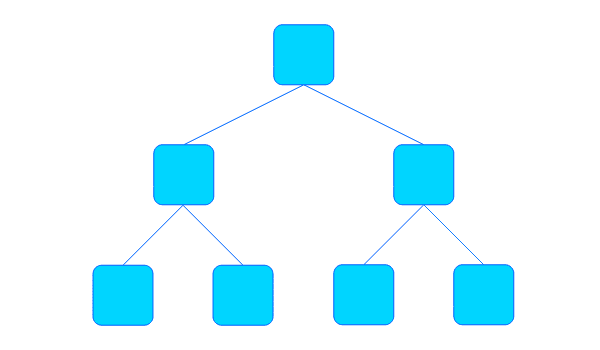
  이진 트리에서 모든 Level에 노드가 가득 차 있는 트리를 포화 이진 트리(Full Binary Tree)라고 합니다.
• 완전 이진 트리(Complete Binary Tree)
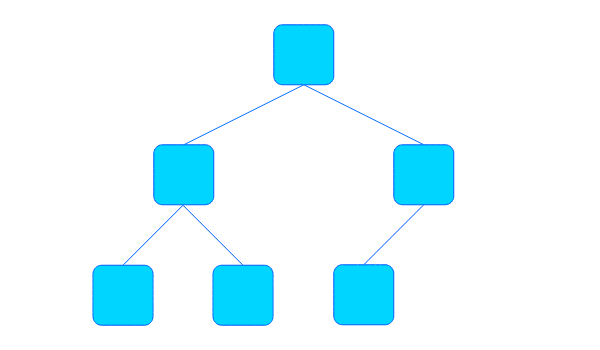
  노드를 추가할 때 왼쪽부터 오른쪽으로 차곡차곡 추가하는 트리를 완전 이진 트리(Complete Binary Tree)라고 합니다. 완전 이진 트리의 마지막 Level을 제외한 부분은 항상 포화 이진 트리 상태입니다.

포화 이진 트리가 완전 이진 트리에 속한다고 볼 수 있지만, 완전 이진 트리는 트리를 생성할 때부터 끝까지 완전 이진 트리의 성격을 유지하는 일종의 노드 관리 방식인 반면, 포화 이진 트리는 언제든지 그 특성을 잃을 수 있는 하나의 상태로 볼 수 있습니다.

• 이진 트리로 일반 트리 구현하기
  일반 트리는 이진 트리를 이용하여 구현할 수 있습니다.
  
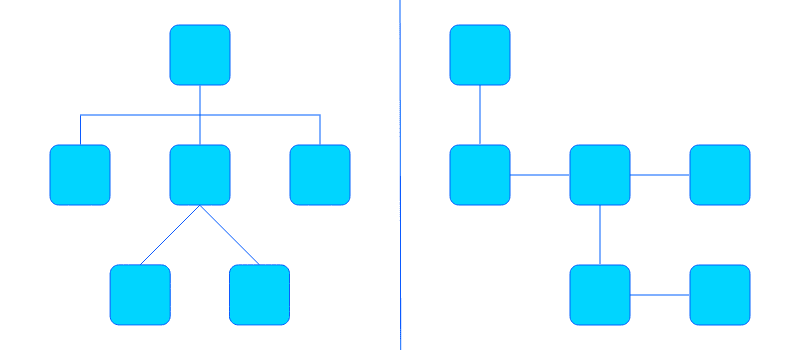
  그림처럼 이진 트리의 Left Child가 자식 노드를, Right Child가 형제 노드를 가리키게 하여 일반 트리를 구현할 수 있습니다. 여기서 부모가 직접적으로 가리키는 자식 노드는 가장 왼쪽에 있는 노드입니다. 다른 형제 노드들은 Right Child 포인터를 이용해 접근할 수 있습니다.

[ 구현 ]

• 포인터를 이용한 이진트리 구현
  포인터를 이용해 이진 트리를 구현하면 하나의 노드는 다음과 같이 생겼습니다.

  template <typename type>
  struct Node
  {
      type data;
      struct Node *left_child;
      struct Node *right_child;
  };

  

  Left Child, Right Child 포인터를 이용해 부모에서 자식으로의 접근이 가능합니다.

• 배열을 이용한 이진트리 구현
  배열을 이용해 이진 트리를 구현하면 별도의 포인터 없이 INDEX의 계산을 통해서 자식 노드에 접근할 수 있습니다.
  
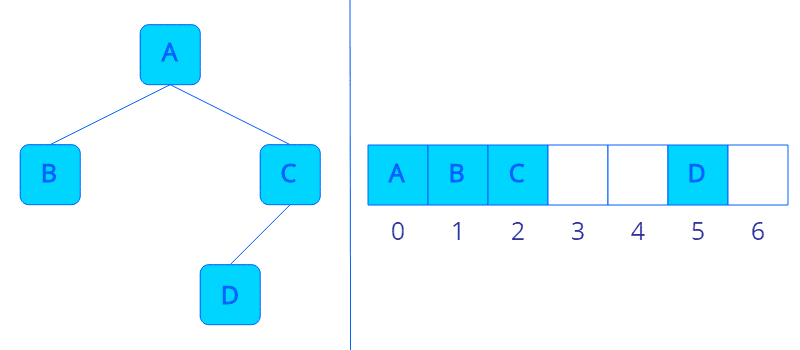
  현재 노드의 INDEX를 K라고 하면 왼쪽 자식 노드의 INDEX는 2*K + 1이며 오른쪽 자식 노드의 INDEX는 2*K + 2가 됩니다. 부모 노드의 INDEX는 (K - 1)/2로 계산할 수 있습니다.
  ※ 하지만, 이렇게 할 경우 트리의 모양에 따라서 배열에 빈 공간이 생겨 메모리가 낭비될 수 있다는 단점이 있습니다. (데이터의 크기가 큰 경우에는 포인터로 인한 메모리 소모보다 훨씬 많은 메모리가 낭비될 수 있습니다.)
  
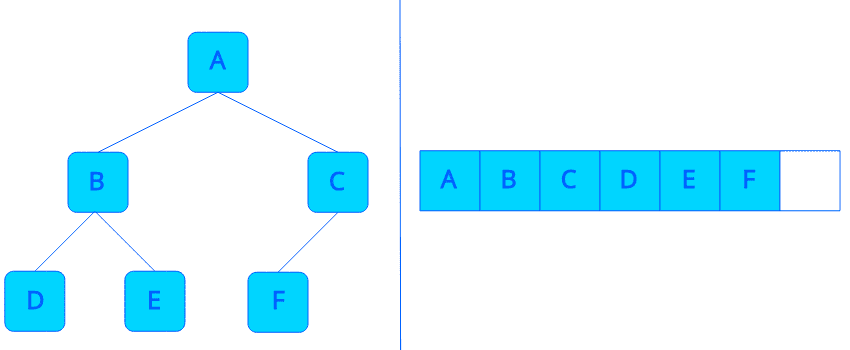
  완전 이진 트리를 구현할 때는 배열로도 빈 공간 없이 효율적으로 구현할 수 있습니다. 따라서 완전 이진 트리를 구현할 때는 보통 배열을 이용해 구현합니다.